Lập trình

KHÁI NIỆM ĐỘ PHỨC TẠP GIẢI THUẬT

Bài viết này cho các người đọc có thể hiểu cơ bản được thế nào là độ phức tạp, và có thể xác định độ phức tạp của một số giải thuật đơn giản.

•         Một bài toán có nhiều giải thuật, vì vậy cần chọn một giải thuật nhanh nhất

•         Thời gian thực hiện giải thuật phụ thuộc:

–        Kích thước dữ liệu: dữ liệu càng lớn thì thời gian xử lý càng chậm. Nếu gọi n là kích thước dữ liệu thì thời gian thực hiện của một giải thuật có thể biểu diễn là một hàm của n: T(n)

–        Phần cứng máy tính

–        Ngôn ngữ, chương trình dịch ngôn ngữ

=> Vì vậy không thể dựa vào thời gian thực hiện giải thuật để xác định T(n), người ta biểu diễn thời gian thực hiện giải thuật chỉ phụ thuộc vào kích thước dữ liệu n.

•         Ví dụ:

–        Thời gian thực hiện một giải thuật là T1(n) = n²

–        Thời gian thực hiện giải thuật khác là T2(n) = 100n

–        Khi n đủ lớn, thời gian thực hiện của giải thuật T2 nhanh hơn giải thuật T1

–        Thời gian thực hiện giải thuật tỉ lệ thuận với n hay tỉ lệ thuận với n² cũng cho ta biết về tốc độ thực hiện của giải thuật đó

Cách đánh giá thời gian thực hiện giải thuật độc lập với máy tính và các yếu tố liên quan đến ngôn ngữ dẫn đến khái niệm gọi là độ phức tạp tính toán của giải thuật

ĐỊNH NGHĨA ĐỘ PHỨC TẠP GIẢI THUẬT

•         Độ phức tạp được ký hiệu bởi chữ “O” lớn

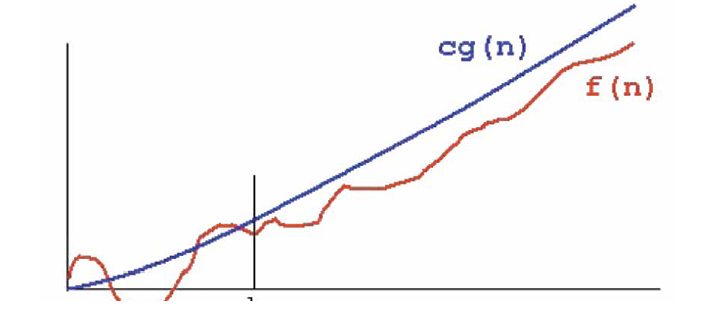
•         Độ phức tạp của hàm f(n) là O(g(n)), nếu tồn tại hằng số dương c và k sao cho f(n) ≤ c.g(n) với bất kỳ n ≥ k

•         Đường tiệm cận c.g(n) với một đường cong là đường mà khoảng cách đến đường cong đã cho tiến đến 0

•         Tìm đường tiệm cận với các tập dữ liệu gọi là phân tích đường tiệm cận

TÍNH CHẤT ĐỘ PHỨC TẠP GIẢI THUẬT

•         Thuật toán có độ phức tạp là hằng số, tức thời gian thực hiện không phụ thuộc vào kích thước dữ liệu n, thì ta ký hiệu độ phức tạp là O(1)

•         Nếu thuật toán có thời gian thực hiện là P(n), với P(n) là một đa thức bậc k thì độ phức tạp tính toán của thuật toán có thể viết là O(n^k)

•         Thuật toán tìm kiếm nhị phân trên mảng đã được sắp xếp hủy một nữa dữ liệu sau mỗi bước thực hiện lặp có độ phức tạp là O(log₂(n)). Nếu thuật toán có thể hủy 90% dữ liệu sau mỗi bước lặp, có độ phức tạp là O(log₁₀(n))

•         Nếu một thuật toán có thời gian thực hiện là log_af(n). Ta nhận thấy log_af(n) = log_ab. log_bf(n), nghĩa là O(log_af(n)) = O(log_bf(n)). Vì vậy ta chỉ ghi độ phức tạp của thuật toán là O(log f(n)) mà không cần ghi cơ số của logarit

Xem link sau về cách xác định độ phức tạp giải thuật đơn giản

http://kcntt.duytan.edu.vn/Home/ArticleDetail/vn/168/2006/xac-dinh-do-phuc-tap-thuat-toan